Designing a tapered spring requires a nuanced understanding of mechanical principles and a keen eye for detail. This comprehensive guide embarks on a journey through the intricate process of tapered spring design, which are known for their conical shape and variable spring rate. From selecting the right materials to understanding the dynamics of tapered spring design.

Key Dimensions of Tapered Spring

When designing a tapered spring, understanding its key dimensions is crucial for ensuring optimal performance and application fit. Unlike regular compression springs, tapered springs feature a unique set of measurements that need careful consideration:
- Outer Diameter (OD):
-
- Largest Outer Diameter (ODL): Typically positioned at the base, providing a stable foundation.
- Smallest Outer Diameter (ODS): Found at the top, contributing to the conical shape.
- Inner Diameter (ID): Measured from the inside width of the smallest coil, crucial for fitting into specific mechanisms.
- Wire Diameter (WD): Thickness of the spring wire, influencing the spring‘s strength and flexibility.
Further, the design of a tapered spring involves several other dimensions that affect its function:
- Mean Diameter (MD): The diameter of the largest active coil, vital for calculating stress at a given load or deflection.
- Free Length (FL): The overall length of the spring when not under any load.
- Total Coils (T/C) and Active Coils (A/C): Determine the spring’s potential deflection and load capacity.
- Solid Height (LH): The length of the spring when fully compressed, important for space-limited applications.
- Pitch (P) and Rise Angle of Coils: Influence the spring rate and how the spring compresses under load.
Understanding these dimensions is foundational to calculating key performance metrics such as the spring rate and load capacity. For instance, the mean diameter (MD) plays a critical role in determining the spring’s behavior under stress. The non-linear nature of tapered springs, attributed to their varying coil diameters, necessitates a detailed analysis of these dimensions to predict performance accurately.
To aid in the design and specification process, consider the following formulae and concepts:
- Spring Rate Calculation: Utilizes the average mean diameter to estimate the spring’s stiffness.
- Solid Length Limit for Closed Ends: Estimated using (H = dN + \nu(ODL – ODS)), where (H) is the solid height, (d) is the wire diameter, (N) is the total number of coils, and (\nu) is a factor accounting for the taper.
By meticulously measuring and understanding these dimensions, engineers and designers can ensure the tapered spring is tailored to meet the specific needs of its application, from achieving the desired deflection and load capacity to fitting within the spatial constraints of the device it supports.
Tapered Spring Design Considerations
When embarking on the tapered spring design, several critical considerations must be taken into account to ensure optimal performance and application fit. These considerations revolve around the spring’s physical dimensions, material selection, and the operational environment in which the spring will function. Below are key factors to consider:
- Physical Dimensions and Specifications:
-
- Outer Diameter (OD): The largest outer diameter is usually at the bottom, offering a stable base and minimizing buckling under compression.
- Inner Diameter (ID) and Wire Diameter (WD): Essential for fitting the spring into specific mechanisms and determining the spring’s strength and flexibility.
- Free Length (FL) and Solid Height (LH): Critical for applications with space limitations, influencing how much the spring can compress.
- Pitch (P) and Helix Angle (α): Affect the spring’s rate and how it compresses under load.
- Material and Environmental Considerations:
-
- Material Selection: Choose materials like music wire, stainless steel, or chrome silicon based on the spring’s required properties, such as tensile strength, corrosion resistance, and temperature tolerance.
- Operational Environment: Consider the environment in which the spring will operate, including factors like temperature, humidity, and potential corrosive elements, to select the most suitable material and finish.
- Engineering and Design Elements:
-
- Buckling Prevention: Utilize the recommended length-to-diameter ratios (L/D) and consider the use of barrel, hourglass, or conical shapes to prevent buckling under load.
- Spring Rate Calculation: An approximate rate can be calculated using the spring’s average mean diameter, keeping in mind that the rate becomes non-linear once larger diameter coils contact each other during compression.
- Stress and Fatigue Life: Determine the uncorrected stress for static applications and aim for 30 to 45 percent of the Material Tensile Strength (MTS) value as a corrected stress target for a long fatigue life.
- Minimizing Resonant Amplitudes: Tapered springs can reduce bouncing amplitudes in vibrating objects due to their progressive contact, enhancing stability in dynamic applications.
By carefully considering these factors, designers can tailor tapered springs to meet the specific needs of their applications, from achieving the desired deflection and load capacity to ensuring durability and reliability in the intended operational environment.
Tapered Spring End Types
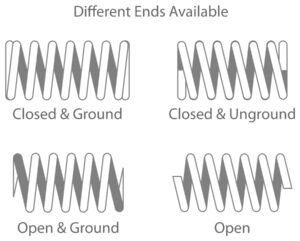
Tapered springs, often recognized for their distinctive conical shape, exhibit a unique characteristic where the coil thickness diminishes towards one end. This design innovation leads to several key features and benefits:
- Versatile End Types: Tapered springs can be manufactured with various end types to suit different application needs, including:
-
- Open ends
- Closed ends
- Close and ground ends
- Double closed ends
Materials Used in Tapered Springs
Tapered springs, also recognized as conical springs, are crafted from a variety of materials, each selected for its unique properties to meet specific operational requirements. The choice of material is pivotal, influencing the spring’s performance, durability, and application suitability. Here’s a breakdown of common materials used in tapered spring manufacturing:
- Music Wire:
-
- Properties: High tensile strength, excellent fatigue life.
- Limitations: Prone to rust in moist environments; not recommended for humid conditions.
- Applications: Widely used in general-purpose applications but avoided in medical or marine environments.
- Stainless Steel (Grades 302, 304, 316, 17-7 PH):
-
- Properties: Resistant to high temperatures (up to 550º F/288º C) and corrosion, making it suitable for challenging conditions.
- Applications: Preferred in medical devices and applications involving high temperatures or corrosive environments.
- Chrome Silicon:
-
- Properties: Superior strength and high-temperature resistance compared to Stainless Steel.
- Limitations: Susceptible to rust when exposed to moisture; not ideal for humid conditions.
- Applications: Used in high-stress applications where strength and temperature resistance are critical.
In addition to these primary materials, tapered springs can also be manufactured from:
- High-Carbon Spring Steels (e.g., oil-tempered): Known for their versatility, cost-effectiveness, and ability to maintain strength at elevated temperatures.
- Alloy Spring Steels (e.g., Chrome Silicon): Excellent for resisting shock loading and cyclic fatigue failure.
- Non-ferrous Materials (Aluminium, Copper, Nickel): Chosen for their corrosion resistance, easy machinability, good thermal and electrical conductivity, and non-magnetic properties. Aluminium, being lightweight, is particularly suitable for aerospace and marine industries, while Copper’s high electrical conductivity makes it ideal for electrical applications. Nickel’s toughness and corrosion resistance lend it to a wide range of uses in spring manufacturing.
Material Finishes:
- Common Finishes: Zinc, Gold Irridite®, Black Oxide, Passivated (upon request), and None (can be plated upon request).
- Specialty Finishes: Rust-resistant finishes, brass, chrome, black powder, and brushed nickel are available to enhance the spring’s appearance, corrosion resistance, and overall performance.
Selecting the right material and finish for a tapered spring is a critical step in the design process, directly impacting the spring’s functionality, longevity, and cost. Environmental factors, operational stresses, and specific application requirements must be carefully considered to ensure optimal material selection.
Calculating Tapered Spring Rate and Load
Calculating the spring rate and load for tapered springs is essential to ensure they meet the specific requirements of their intended application. To facilitate this process, tools such as the Spring Creator calculator are invaluable. Here’s a breakdown of the key components and formulas involved in these calculations:
- Spring Rate Calculation:
-
- Formula: (k = \frac{Gd^4}{8D^3na})
-
- Where:
-
- (G) = Shear modulus of the material
- (d) = Spring wire diameter
- (D) = Mean diameter of the spring
- (na) = Number of active coils
- This formula helps determine the stiffness of a spring, indicating how much force is needed to compress it by a certain distance.
- Load Calculation:
-
- Formula: (P = \frac{\pi d^3 G}{8D^3})
-
- Where:
-
- (P) = Load on the spring
- (d) = Wire diameter
- (G) = Shear modulus of elasticity
- (D) = Mean coil diameter
- This calculation provides the force applied to the spring and the distance it will travel under that force, crucial for designing springs that can withstand their working load limits.
- Solid Length and Stress Calculations:
-
- For Solid Length (HS):
-
- Compression Springs: (HS = (Nt-1)d + (t1 + t2))
- Maximum Solid Length: (HS = Nt \times d_{max})
-
- Where (Nt) = Total coils, (d_{max}) = Material diameter with maximum tolerance, and (t1 + t2) = Sum of the thicknesses of the coil ends.
- Torsional Stress ((\tau)): ( \tau = \frac{Pd}{2A} )
-
- Corrected Torsional Stress ((\tau_c)) = ( \tau \frac{(4c-1)}{(4c-4)} )
-
- Where (c) = Spring index, (P) = Load, (d) = Wire diameter, and (A) = Cross-sectional area of the wire.
In addition to these formulas, the Spring Store offers tools like the Spring Finder and Spring Rate Calculator, which simplify the process of finding and calculating the specifications for both stock and custom tapered springs. These calculators provide instant quotes and allow for adjustments based on the spring’s material type, wire diameter, outer diameter, and other key dimensions. Whether designing compression or extension springs, these tools ensure that engineers can accurately determine the spring rate, load capacity, and other critical parameters to match their specific application needs.
Tapered Spring Stability and Buckling
In the realm of mechanical design, ensuring the stability of tapered springs and preventing buckling under compression is paramount. Tapered springs, with their unique conical shape, offer inherent advantages in this regard, thanks to the nesting effect. This effect allows coils to fit within each other when compressed, significantly reducing the risk of buckling. Buckling, a deformation that occurs in a non-axial direction under compression, can lead to spring failure and, consequently, the malfunctioning of the application it supports.
Understanding and managing the slenderness ratio is crucial in the design of tapered springs to avoid buckling. The slenderness ratio, defined as the proportion of the mean diameter to its length, serves as a critical parameter. A spring with a mean diameter over three times its length is prone to buckling. Design strategies to mitigate this include:
- Utilizing custom springs with adjusted dimensions for specific applications.
- Adjusting the placement of stock springs within the assembly to ensure optimal load distribution.
- Designing springs with a length exceeding the critical buckling length (LK) to enhance stability.
- Ensuring regular maintenance and inspection routines to detect and rectify potential issues early.
Moreover, practical design adjustments can further bolster the stability of tapered springs. These adjustments, aimed at influencing the spring’s slenderness ratio and load distribution, include:
- Adding more coils: Increases the spring’s overall length and reduces the slenderness ratio.
- Decreasing the free length: Shortens the distance between coils, enhancing stability.
- Increasing the outer diameter: Provides a broader base, reducing the likelihood of lateral movement.
Incorporating these design considerations ensures that tapered springs can deliver their intended benefits, such as a progressive spring rate, space efficiency, reduced solid height, and enhanced damping characteristics, without succumbing to buckling. By carefully selecting the spring’s dimensions, material, and by considering its operational environment, designers can leverage the unique advantages of tapered springs for a wide range of applications.
The Telescope Effect
The telescope effect, also known as nesting, is a distinctive feature of certain tapered springs, enabling them to fully collapse into a minimal solid height equivalent to the spring’s wire diameter when compressed. This characteristic is particularly advantageous in applications where space constraints limit the length of the spring, yet a significant amount of deflection or travel is required. Here’s a closer look at how this effect is achieved and its benefits:
- Mechanism of the Telescope Effect:
-
- The phenomenon occurs when the inner diameter of one coil is larger than the outer diameter of the coil immediately below it. This size difference allows each smaller coil to compress into the larger coil’s inner diameter seamlessly.
- As the spring compresses, the coils nest within each other, ultimately reducing the spring’s overall height to just the wire diameter, assuming the material has sufficient elasticity.
- Advantages of the Telescope Effect:
-
- Space Efficiency: Maximizes the use of available space by allowing the spring to occupy minimal volume when fully compressed.
- Enhanced Deflection: Provides greater travel or deflection than would be possible with a spring of similar dimensions but without the nesting capability.
- Design Flexibility: Enables engineers to design compact assemblies without compromising on the functional requirements of the spring.
For those looking to incorporate tapered springs with the telescope effect into their projects, understanding the precise dimensions and configurations is crucial. The design process involves careful adjustment of the diameters of each coil to ensure the spring can fully collapse under compression. Custom-made tapered springs can be designed to meet specific requirements, offering tailored solutions for unique applications.
- Further Resources:
-
- For a deeper understanding of tapered spring terminology and dimensions, exploring resources on tapered spring terminology and dimensions is recommended.
- In cases where off-the-shelf solutions do not suffice, contacting specialists for custom-made springs can provide the necessary customization to achieve the desired telescope effect and performance.
This innovative feature of tapered springs opens up new possibilities for mechanical design, particularly in space-constrained environments where the ability to achieve significant deflection without increasing the spring’s free length is invaluable.
Conclusion
Through the comprehensive examination of tapered springs, this article has showcased the intricate properties that make these components indispensable in the realm of mechanical design. From the initial selection of materials like spring steel and beryllium copper, which ensure durability and performance, to the detailed exploration of key design considerations such as spring rate and load capacity, we have unfolded the multifaceted nature of these springs. The pivotal ‘telescope effect’ and the nuanced manufacturing processes further highlight the innovation and precision involved in producing tapered springs tailored for applications where space is limited, and stability is critical.



